Network Analysis
Part 1: to be completed at home before the lab
During this practical, we will cover an introduction to network analysis. We cover the following topics:
- metrics to describe network,
- centrality indices,
- community detection,
- network visualization.
We will mainly use the igraph package.
You can download the student zip including all needed files for this lab here.
Note: the completed homework has to be handed in on BlackBoard and will be graded (pass/fail, counting towards your grade for individual assignment). The deadline is two hours before the start of your lab. Hand-in should be a PDF file. If you know how to knit pdf files, you can hand in the knitted pdf file. However, if you have not done this before, you are advised to knit to a html file as specified below, and within the html browser, ‘print’ your file as a pdf file.
For this practical, you will need the following packages:
#install.packages("tidyverse")
library(readr)
library(tidyverse)
library(ggplot2)
#install.packages("igraph")
library(igraph)
#install.packages("RColorBrewer")
library(RColorBrewer)
#install.packages("sbm")
library(sbm)
#install.packages("fossil")
library(fossil)
set.seed(42)We are going to use the high school temporal contacts dataset, created in the context of the SocioPatterns project.
The dataset is publicly available in the repository Netzschleuder and it corresponds to the contacts and friendship relations between students in a high school in Marseilles, France, in December 2013. The contacts are measured in four different ways:
- with proximity devices (see folder
data/proximity), - through contact diaries (see folder
data/diaries), - from reported friendships in a survey (see folder
data/survey), - from Facebook friendships (see folder
data/facebook).
Each folder contains the edgelist (edges.csv), with the source node, target node, and additional properties (interaction strength or time at which the interaction happened). The nodes.csv file contains the node’s (students) IDs, the class they belong to, and their gender. In this lab, we will use the proximity data, but the same analysis can be repeated for the other three datasets in a similar way.
Reading a network file
1a. Read the edgelist file (edges.csv in the data/proximity folder) and store it in the variable edge_list. The csv file contains an edge list with two columns: source node (one student), target node (the other student), and the time at which the interaction happened. To load it, use the function read_csv from the readr package. What is the advantage of storing the network using an edge list, rather than in an adjacency matrix? Is the difference more relevant in the case of sparse or dense networks?
Answer:
1b. Read also the node properties file (nodes.csv in the data/proximity folder) and store it in the variable node_prop. What information is in this file?
Answer:
- Network creation: Create the network using the
edge_listand the functiongraph_from_data_framefrom theigraphpackage. Store the graph in the variableg. If you look for?graph_from_data_frameyou can find all the arguments of this function. Your graph will be anundirectedgraph, and you can add the node properties by setting theverticesargument to thenode_propvariable
Network description I
3a. Descriptive statistics: count how many students are there per class (using group_by), using the node_prop variable
3b. Descriptive statistics: print (a) the number of nodes (function vcount) and (b) the number of edges (function ecount) (c) the longest path on the network (diameter, setting the variable unconnected to false), (d) the average path length (mean_distance, setting the variable unconnected to false), (e) the global clustering coefficient (transitivity).
3c. How do you interpret the results of the diameter and the average path length? How do you interpret the clustering coefficient?
Part 2: during the lab
Network manipulaton
4a. Simplify network: the current network has isolated components (some students do not interact with anybody, maybe because they were sick). Print the number of components (function components). Identify the isolated nodes with (V(g)$name[degree(g) == 0]) and remove (delete_vertices) those nodes from the network. Check again the number of connected components in the new network.
4b. Simplify network: the current network has self-loops (i.e. if there is a record of a student’s proximity with themselves) and duplicated edges (because students interact several times). Print if there are self-loops (function any_multiple), and the number of duplicated edges (function which_multiple). Then remove self-loops (function simplify) and collapse all duplicated edges into one weighted edge (simplify(g, edge.attr.comb = "sum"). Store the new graph to the variable g_simple
4c. Check again the number of connected components in the new network. Compute the descriptive statistics for the new network. Did the values change? Why? Is it always a good choice to focus on the largest connected component? Provide an example of research question when this is not the case.
Answer:
Network description II
5a. Degree distribution: use function degree to store the degree of each node in the network in the variable degree_dist. What’s the mean degree and its standard deviation? Plot the degree_dist as a histogram with ggplot (geom_histogram).
5b. Degree distribution: compare the degree distribution to the class sizes. How do you interpret these results?
Answer:
Network visualization
6a. Network Visualization: visualize the simplified network using the function plot.
6b. This is a bit ugly, let’s assign different colors to school classes. You can use the following code for this
# Color palette
palette <- rainbow(length(unique(V(g_simple)$class)))
# Create a color mapping for each node to their class
color_mapping <- setNames(palette, unique(V(g_simple)$class))
# Map the node colors based on the class
node_colors <- color_mapping[V(g_simple)$class]
plot(g_simple, vertex.color = node_colors)
# Adding a legend
legend("topright", legend = names(color_mapping), fill = palette, title = "Class")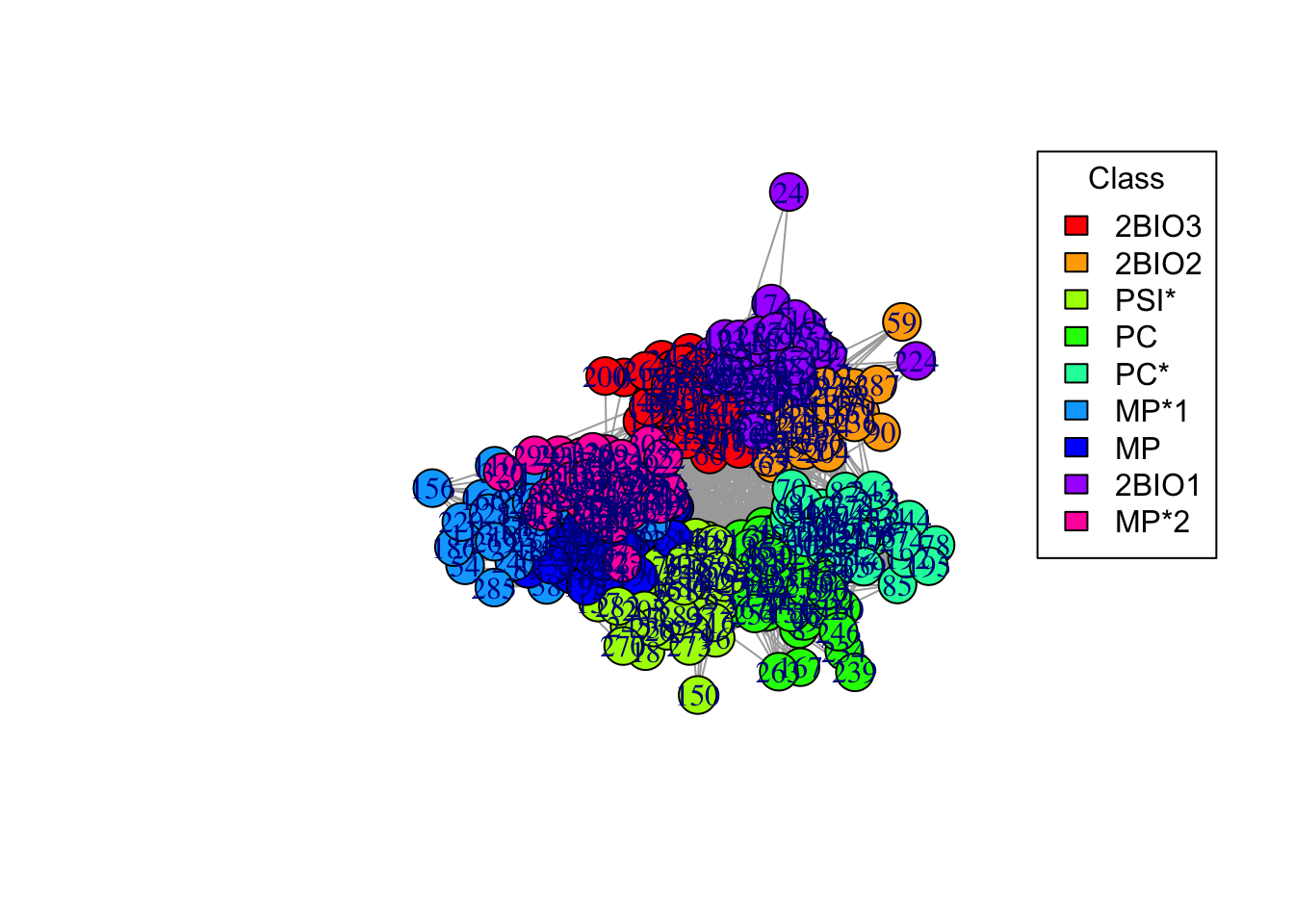
6c. Now, add a layout. Use a “spring” algorithm for visualization, where nodes that are connected get pushed together, and nodes that are not connected get pushed apart. Store the coordinates of each node (coords = layout_with_fr(g_simple)), to plot them in the same position in the next plots (you can experiment with different layout algorithms, see ?layout_).
6d. Make the plot prettier! Play with the plot function options (e.g., vertex.size = 5, vertex.label = NA, edge.width = 0.1, edge.arrow.size = 0) until you are happy with the results. Make sure you have a legend
6e. Do students in the same class interact more? Why are there so many connections between different classes? Do you notice any pattern?
Answer:
Centrality measures
7a. Centrality measures: during the lecture we discussed different types of centrality measures, that are useful to quantify the importance of nodes in the network. The most widely used ones are: degree, betweenness, closeness, and pagerank centrality. Explain each measure and how it differs from the others. Compute all the centrality measures (with functions degree, betweenness, closeness, and page_rank). Find the most central nodes according to these measures (which(centrality == max(centrality))). You can use the pre-made function calculate_and_print_max_centrality below. Is the same node the most central node by all definitions?
- Degree:
- Betweenness:
- Closeness:
- Pagerank:
calculate_and_print_max_centrality <- function(graph, centrality_type) {
# Calculate the specified centrality based on the type provided
centrality <- switch(centrality_type,
"degree" = degree(graph),
"betweenness" = betweenness(graph),
"closeness" = closeness(graph),
"pagerank" = page_rank(graph)$vector,
stop("Invalid centrality type"))
# Find the node(s) with the highest centrality
max_value <- max(centrality)
highest_nodes <- which(centrality == max_value)
# Print results
cat(sprintf("Node id(s) with highest %s centrality: %s\n", centrality_type, toString(highest_nodes)))
}7b. Let’s label those nodes. You can again use the plot function to create the plot and set vertex.label = labels. Also, set vertex.label.size=1000 to be able to see the labels
Community detection
8a. Community detection: we would like to detect communities in the network. Let’s start with the cluster_leiden function, which creates communities that maximize a metric (either CPM or modularity). Create the communities using modularity (see ?cluster_leiden) and store the results in a variable (e.g. modularity).
8b. Now, plot the network with the communities. You can just visualize the network using the function plot(commdet, g_simple), where commdet may be substituted with the variable name where you stored the community detection results. Remember to fix layout = coords to plot the nodes always in the same position.
8c. How do the communities align with the classrooms (question 6)?
Answer:
9a. Community detection: There are other methods implemented in igraph: cluster_spinglass, based on the spinglass model from statistical mechanics; cluster_walktrap, based on random walks; and cluster_label_prop, based on labeling all nodes and then updating the labels by majority voting. We will also employ the SBM (Stochastic Block Model) from the homonym package. Use these methods to find communities (e.g. cluster_spinglass(g_simple)). Store the results for each method in different variables. There are more methods available in igraph, feel free to try others. For the SBM we provide the code below. It may take a few minutes.
adj <- as_adjacency_matrix(g_simple, sparse=FALSE)
simple_sbm <- estimateSimpleSBM(adj, 'bernoulli', estimOptions = list(verbose = 0, plot = FALSE))9b. Compare communities visually: let’s visualize the network as in the modularity case above. For SBM we provide code below.
#Color palette
palette <- rainbow(length(unique(simple_sbm$memberships)))
#Create a color mapping for each node to their class
color_mapping <- setNames(palette, unique(simple_sbm$memberships))
#Map the node colors based on the class
node_colors <- color_mapping[simple_sbm$memberships]
plot(g_simple, layout=coords, vertex.color = node_colors, vertex.size=5, vertex.label=NA, edge.arrow.size=0, edge.width=0.1, edge.color="grey")
title(main ="SBM")
9c. How do the community assignments produced by the algorithms comparing to the division of students in classrooms (question 6)?
Answer:
10a. EXTRA QUESTION: Compare the similarity between the communities detected and the classrooms. Use the Rand Index, a measure that quantifies the similarity between two data clusterings by considering all pairs of elements and checking whether the pair is either assigned to the same or different clusters in both clusterings. Compute the Rand Index between the classroom assignment (as.integer(factor(V(g_simple)$class))), which we consider now as ground truth, and the community assignment (commdet$membership) for each method. Use the function rand.index from the fossil package. Give a formal definition of the Rand Index. Which method(s) is better capturing the “true” subdivision?
Answer:
10b. There is a corrected-by-chance version of the Rand Index called Adjusted Rand Index (adj.rand.index(group1, group2)). Give the definition and repeat the same done for the RI. Are the results different? Which method is best?
Answer: